Hyperrhiz 26
Classification of Mathematical Poetry
Radoslav Rochallyi
Citation: Rochallyi, Radoslav. “Classification of Mathematical Poetry.” Hyperrhiz: New Media Cultures, no. 26, 2023. doi:10.20415/hyp/026.a01
Abstract: In this statement I aim to create at least a partial classification of mathematical poetry as part of a large group of experimental poetry. I have created a primary classification according to pure mathematics, knowing that it is incomplete and can be extended within and towards other mathematical disciplines, such as applied mathematics or borderline disciplines. All unfamiliar artistic forms in the text are poems themselves. However, it can be used for an analysis of any poem.
Keywords: Mathematical poetry, classification, vector poetry, equation poetry.
Introduction
The connection between mathematics and poetry is an entirely natural thing. Mathematics and poetry share symbols (symbolism), algorithmic basis, structures, patterns, and symmetry. If we look at poetry carefully, we find that nearly every formal rule in poetry is mathematical. This restriction defines the form of poetry. Thus, it can be said that no form of poetry is without mathematics. However, more than just form, mathematics and poetry require great imagination. Also, for some, numbers carry their special meaning, like “666” representing “the number of the beast” or evil, and “1” representing the best or the loneliest number. Therefore, mathematics provides a refreshing new take on writing poetry. Structurally and visually, mathematical poetry is relatively simple but effective. It works quickly because the limits are only in the poem's form.
I do not consider mathematical poetry to be poetry about mathematics; the content of the poetry does not have mathematical meaning. Instead, mathematical poetry means poetry whose form is determined/defined by a mathematical rule, pattern, symbol, or structure—some mathematical or geometric constraint. Poems with a mathematical structure do not necessarily have to be poems in the forms of a pyramid, a triangle, a square, or poems depicting natural objects; they can also depict relations, as in equations. Mathematical poetry has a long tradition, especially visual poetry. Since the nineties of the twentieth century, equational poetry, applied mainly as visual poetry, has begun appearing in Kaz Maslanka's works. Also emerging is a poetry of applied mathematics, such as Mez Breeze‘s Code Poetry and Alan Sondheim‘s Codework, both of which use code structures.
If we take a closer look at poetry as such, the formal structures in poetry often draw upon logic and symmetries that reflect mathematical structures. This restriction defines the form of poetry. Hence, it can be said that (almost) no form of poetry can do without mathematics. Mathematics and poetry require great imagination. They have symbolism, algorithmic basis, structures, formulas, and symmetry. Combining the two is natural, as is reading and studying their patterns. I believe the mathematical structure of a poem should enhance the poem‘s meaning.
Classification of Mathematical Poetry
In this section, I will try to classify mathematical poetry, being aware of the imperfection and the possibility of improving the table and classification.
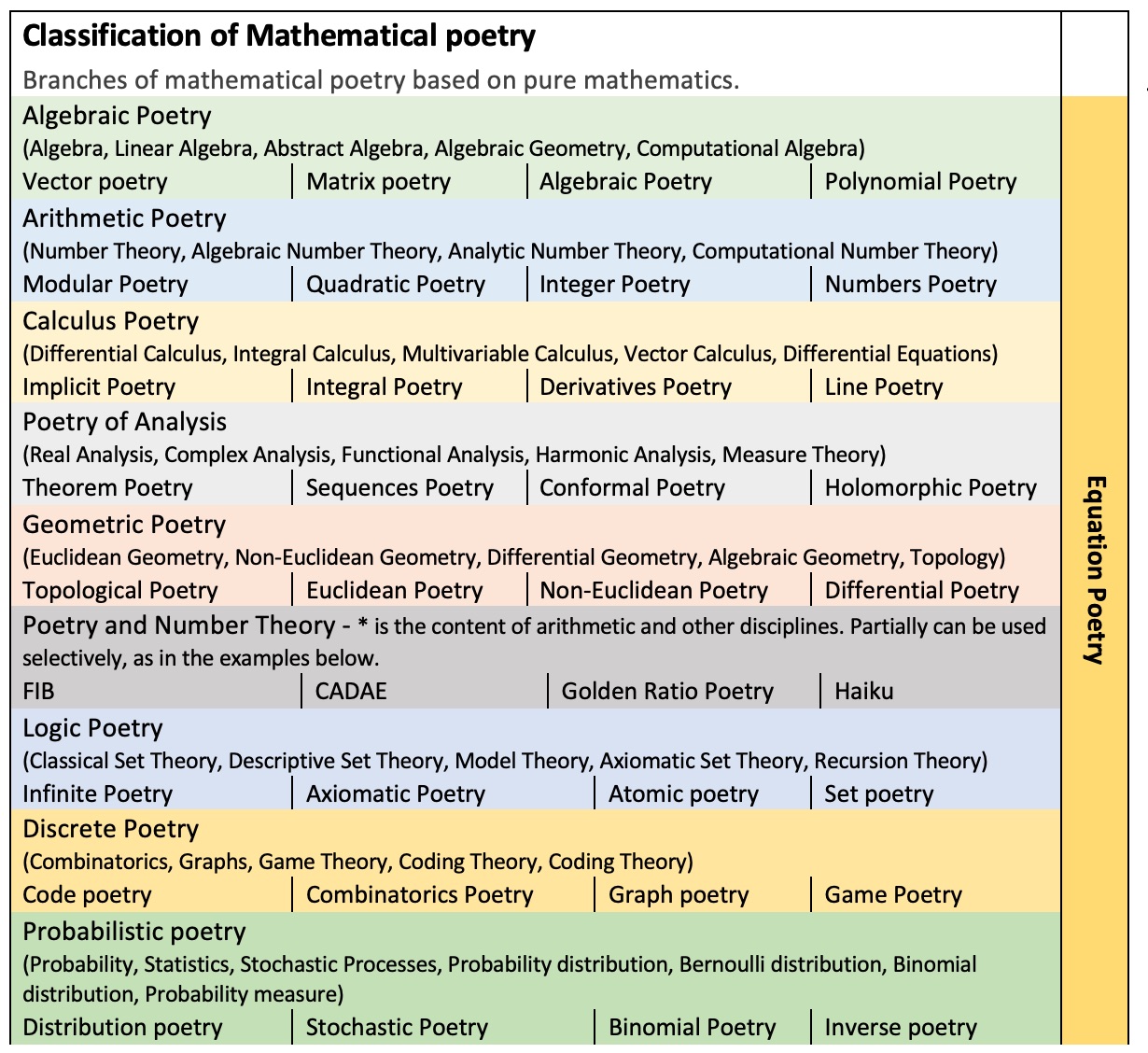
In the remainder of this statement, I will introduce the reader to examples of mathematical poetry developed in particular in my own work, characterizing each piece according to its formal mathematical rules and structures.
Selected Examples
I: Algebraic Poetry
(Algebra, Linear Algebra, Abstract Algebra, Algebraic Geometry, Computational Algebra, etc.)
At the beginning, I must say that I will not work with vectors in the same way as the scientific field of machine learning or NLP (Natural Language Processing) works with them - where the text is a sequence of discrete symbols.For my needs, a vector is a quantity (in our case, a sentence) that has a magnitude and a direction, and which is usually represented by a directed arrow line, the length of which represents the direction in space, that is, an element of the vector space. And thus the vector semantics itself, which represents a sentence in a multidimensional vector space, may or may not represent a specific sentiment in relation to other sentences in the space.So my application of vectors is not exact, it is more artistic than mathematical.
Selected parts to analyze for use as a basis for algebraic poetry:
Vector poetry (Vectors as a method of creating poetry and vectorization of poetry through vector space-VSP):
The essence of vector poetry is to capture states, space, and time alongside the poem's central message. We can say that Vector poetry is a mathematical poem that uses the properties and structure of vector space to create a concise but poetic form of expression. This type of poetry combines the mathematical and poetic worlds, which allows for a holistic understanding of both concepts. It can explore different vectors, such as time and space vectors. Vector poetry has many possibilities for the author, allowing them to create exciting verses that draw from the mathematical concepts surrounding them.
We can achieve an emotional effect in the following ways:
1. Moving a word or phrase along a grid of vector space to create a visual effect and especially an emotional effect
2. Using mathematical equations to create shapes and movementsIn vector poetry, words are arranged in a specific way to represent the poem's meaning visually. Each word or sentence is represented by a line that points in a particular direction and has a certain length. The length of each line represents the importance of that word concerning other words in the poem. The focus in each line means how strongly that word relates to other words in the poem. For example, if we wanted to express “love” as a vector, you could draw an arrow pointing up because love is positive and good; however, if you wanted to represent 'hate' with negative connotations, you would draw a downward arrow instead. Vector poetry is possible because of the way vectors are used in mathematics. Vectors represent the direction and magnitude of a force and can be used to describe both physical forces and abstract concepts.
I propose two methods for creating vector poetry or for using vectors to convey meaning: using vectors to describe the movement of emotion and using vectors to create the position of expressed feelings in the author's space. The first method, describing the shape of the movement of the emotion, is the most direct. The poet chooses a word and creates a vector that strengthens, complements, and explains the feeling. This method is the most natural and is universally applicable to any artistic expression. The second method, describing the position of defined objects and states in the space of the poet's expression, is more complex. The poet takes the sentence they want to say and creates a vector representation of its movement or the movement of its parts. In contrast, the vector space represents the author's interior and recent experience.
Vector poetry can, of course, be created in different ways. The examples used here are just some of the possibilities, and should serve as inspiration. Nevertheless, I believe that vector poetry could be effectively established as a new form.
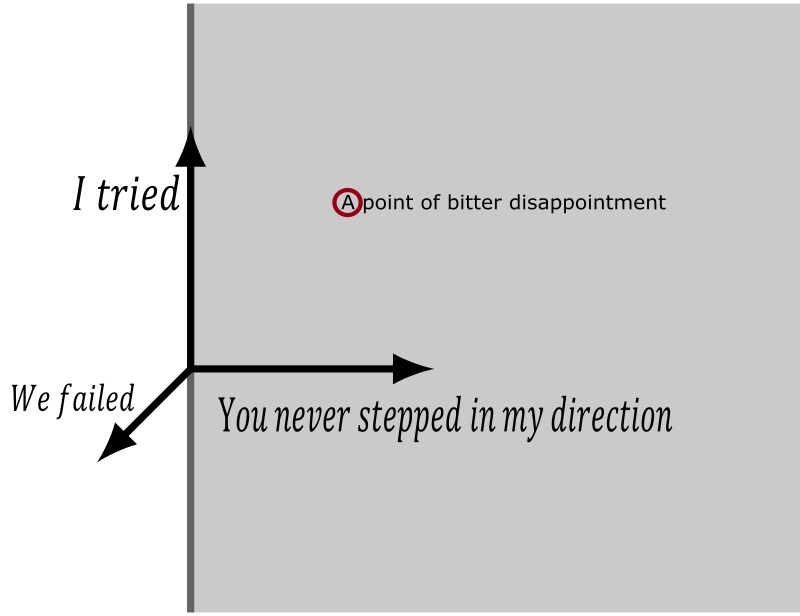
Figure 1. Example of transcription into vector poetry. Image modified from “Dielectric half space of z>0. Electric susceptibility of the dielectric is chi,” Wikimedia Commons. Radoslav Rochallyi, 2022. 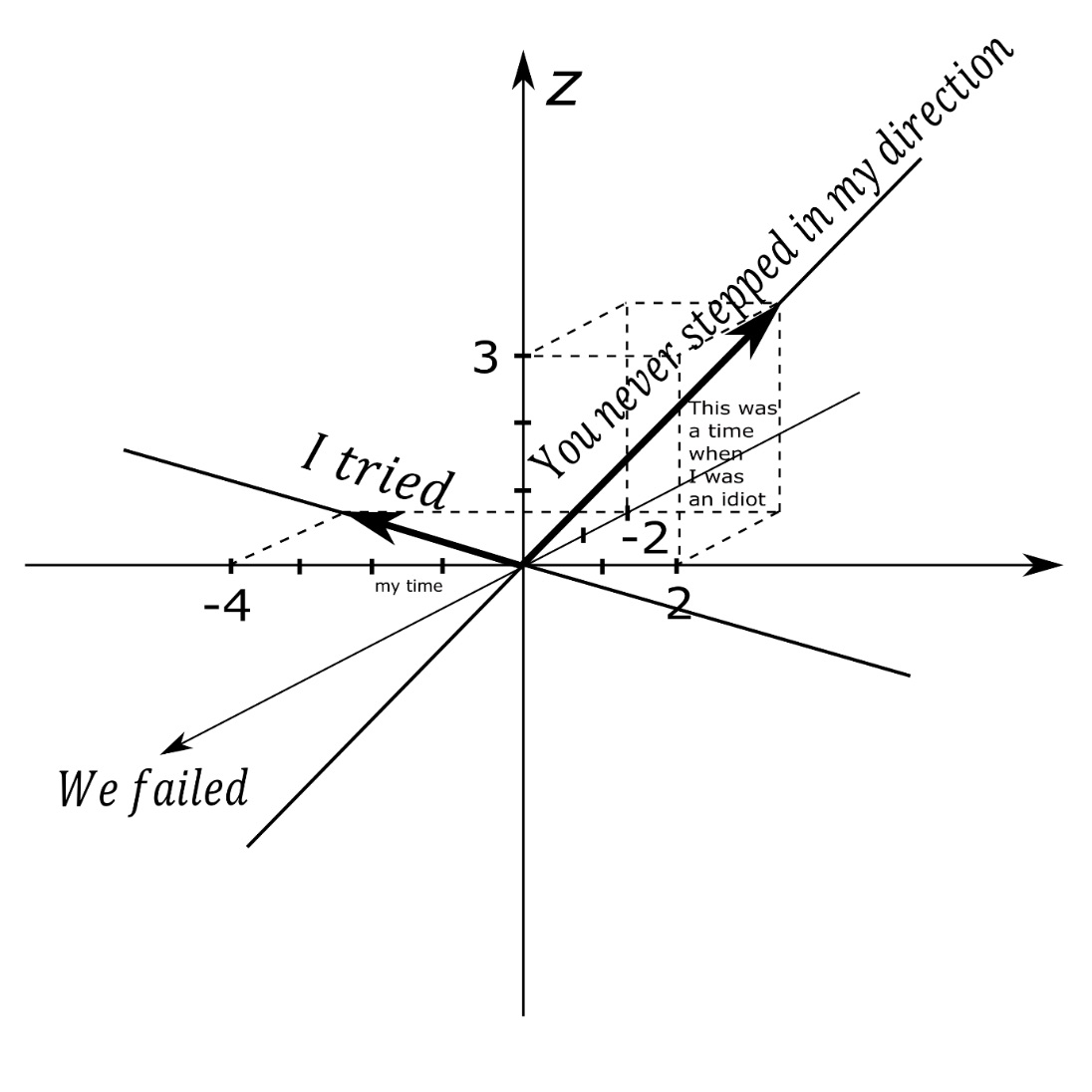
Figure 2. Example of transcription into vector poetry in vector space. Image modified from “Geometrical interpretation of a linear span of vector in 3D Euclidean space. Linear spans of two vectors are depicted,” Wikimedia Commons. Radoslav Rochallyi, 2022. 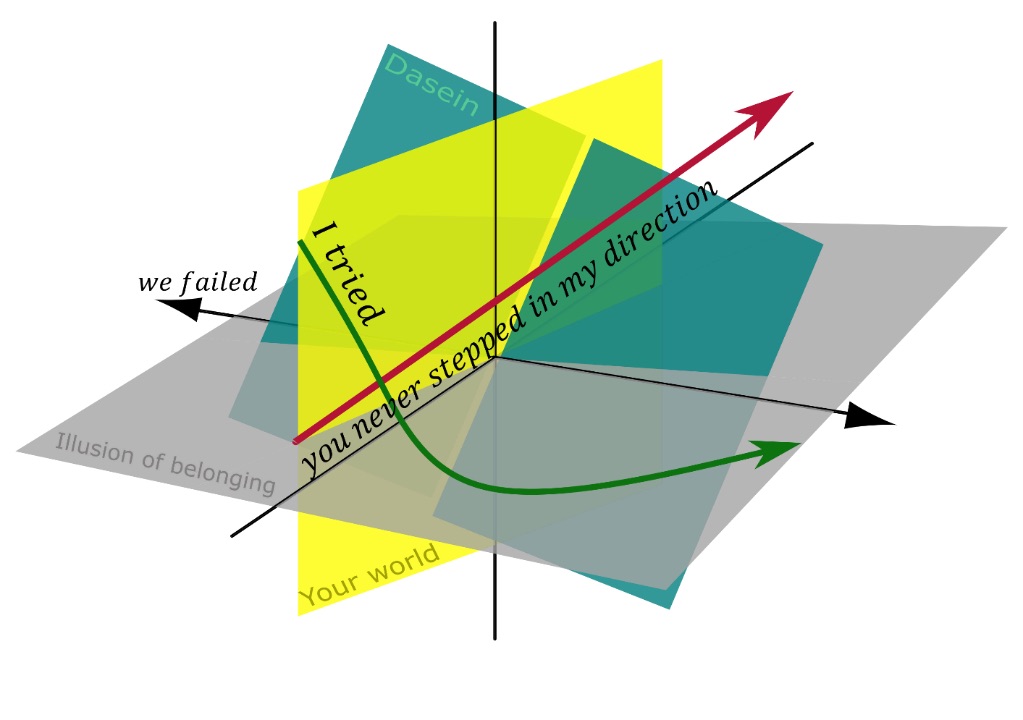
Figure 3. Example of transcription into vector poetry in vector space. Image modified from “linear and vector and tensor space and streaming,” Wikimedia Commons. Radoslav Rochallyi, 2022. -
Matrix poetry: The essence of matrix poetry is the representation of emotional or relational subjects or states divided into separate parts. It is a simple form that can replace classical stanzas in poetry.
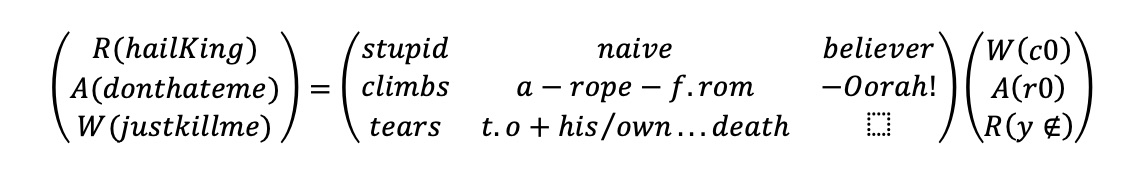
Figure 4. Radoslav Rochallyi, “íllyen és hárború! (long live the war!).“ # mathaeata, 2021, ISBN: 978-8097373719.
II: Calculus Poetry
(Differential Calculus, Integral Calculus, Multivariable Calculus, Vector Calculus, Differential Equations, etc.) Selected parts to analyze for use as a basis for poetry:
-
Differential Poetry: The essence of differential poetry cannot be a different number. However, we can use it as a model for describing states and their changes. We could probably insert the function's derivative at the selected initial state/emotion and describe the function's rate of change near this input value of the particular state/emotion. It would be most appropriate to use a graphic representation. The figure below could describe the movement of an emotion/state, while the axes could define the specifics and variations of that state.
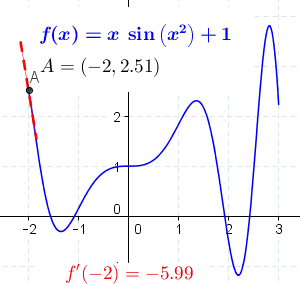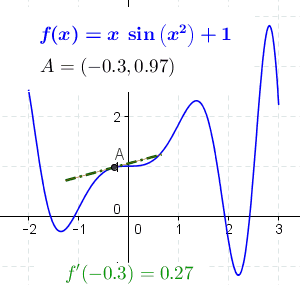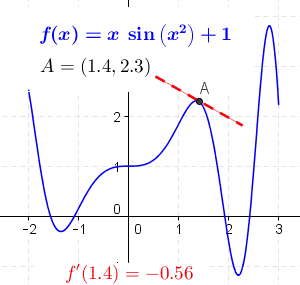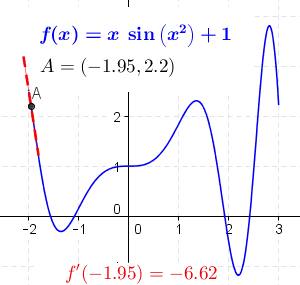
Figure 5. “The derivative at different points of a differentiable function.” Wikimedia Commons. Integral Poetry: The essence of integral poetry is to amplify words/sentences in a way that describes the shift in meaning, depth of emotion, and other positive and negative changes in the subject's experience.
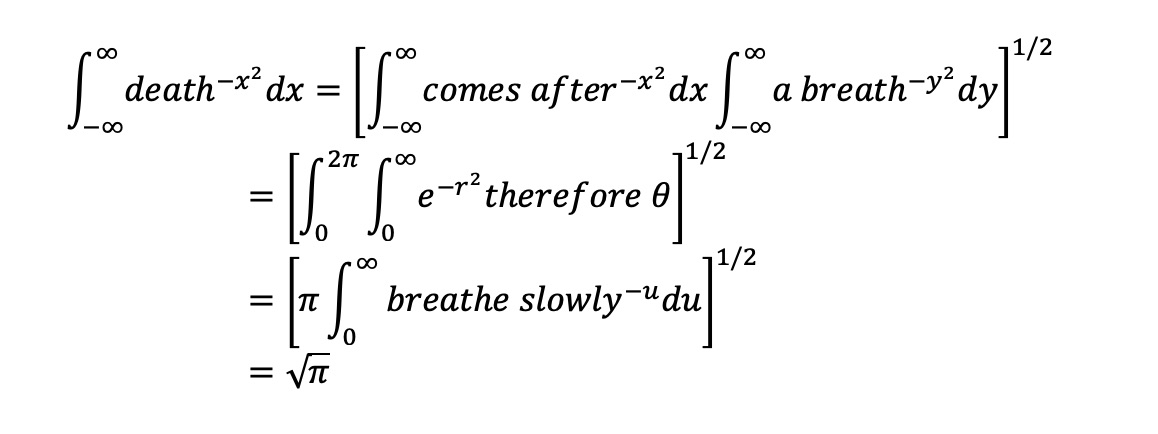
Figure 6. Radoslav Rochallyi, “where the parched scythe of fate begs for mercy.“ # mathaeata, 2021, ISBN: 978-8097373719.
III: Poetry of Analysis
(Real Analysis, Complex Analysis, Functional Analysis, Harmonic Analysis, Measure Theory, etc.)
The essence of Poetry Analysis can be continuous functions and limits. We can also use it as a basis for expressing poetic integration, measure, and infinite sequences directly in the poem, or similar to Vector poetry as a form for placing the poem in the context space.Selected parts to analyze for use as a basis for poetry:
Sequences Poetry: The essence of Sequential Poetry is to display the meaning but also the elements of the poem in an orderly manner, in such a way that the order of words/terms and elements matters, and at the same time in such a way that the same elements can appear several times in different positions in the sequence. Sequential poetry is very close to standard colloquial syntax. An important part is the limits that define the end or infinity of the sequence.

Figure 7. Radoslav Rochallyi, 2023. -
Poetry of Harmonic analysis: The essence of the Poetry of Harmonic Analysis is the representation of emotional signals or changes. Possible use is a visual element and an explicitly described state change over time. Theoretically, we can modify the Fourier transform to create precise Equation poetry. On the contrary, the graphic representation contains an implicit principle of indeterminacy in the environment of the poem's location. The application is also possible as pure visual poetry without words.
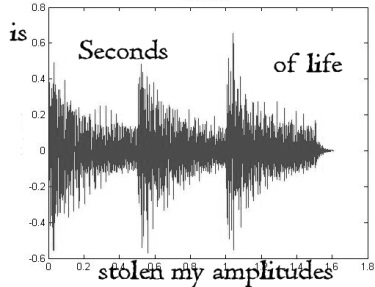
Figure 8. Radoslav Rochallyi, “separate.“ # mathaeata, 2021, ISBN: 978-8097373719.
IV: Geometric Poetry
(Euclidean Geometry, Non-Euclidean Geometry, Differential Geometry, Algebraic Geometry, Topology, etc.) Selected parts to analyze for use as a basis for poetry:
Topological Poetry: The essence of Topological Poetry is depicting a geometric object as a basis for classical, concrete, or visual poetry, where both spatial elements and meaningful elements are preserved. In the case of using a dynamic display of deformations, the meaningful spatial part remains preserved.

Figure 9. Radoslav Rochallyi, 2023. -
Euclidean Poetry: The essence of Euclidean Poetry is the depiction of a geometric object as a part or addition to the poem. Most often used for shaping text into various geometric and realistic patterns. It is the oldest form of mathematical poetry. The essential introducer was Guillaume Apollinaire and his Calligrams, printed in 1918.

Figure 10. Radoslav Rochallyi, 2022. “narcissus, Golden Divine.” Brno: Tribun EU, 34 p. ISBN 978-80-263-0877-5.
V: Poetry and Number Theory
(FIB, CADAE, Golden Ratio Poetry). Selected part to analyze for use as a basis for poetry:
-
Golden Ratio Poetry: The Golden Ratio Poetry is written according to a strict structure based on the golden number 1.618034. A typical representative form of six (nonempty) lines, 1/6/1/8/0/3/4—with the number of words or syllables per line corresponding to the digits of the golden number. The only limitation of “Golden Ratio Poetry” is that the number of words or syllables follows the sequence of digits in 1.618034. Examples of structural mathematical poetry according to φ = 1.618034. The form of poetry based on this number may be as follows:

Figure 11. Radoslav Rochallyi, 2023. Sample according to the number of syllables. Or, according to the number of words:

Figure 12. Radoslav Rochallyi, 2015. “A Blue Night, Golden Divin.”
VI: Logic Poetry
(Classical Set Theory, Descriptive Set Theory, Model Theory, Axiomatic Set Theory, Recursion Theory, etc.) Selected parts to analyze for use as a basis for poetry:
Atomic Poetry: The essence of Atomic Poetry lies in the demand to create poetry with a clear meaning. In logic and philosophy, an atomic sentence is a type of declarative sentence that is either true or false and cannot be broken down into other, more straightforward sentences. This kind of mathematical poetry can be understood as an attempt to eliminate indeterminacy in the text. This form of poetry is suitable for short-word poems or one-sentence poems. It can also be used for poems where statements - sentences - are independent. In The Philosophy of Logic, Willard Van Orman Quine writes that from a logical analysis point of view, the Truth or falsity of sentences, in general, is determined by only two things: the logical form of the sentence and the Truth or falsity of its simple sentences. The Truth or falsity of an atomic sentence is not a matter within the scope of logic itself but rather whatever art or science the content of the atomic sentence happens to be talking about. Of course, having such a radical demand for art would be very limiting. Atomic Poetry insists on statement-manifest clarity rather than formal limitation. Moreover, as with equational poetry, we can apply these restrictions in full breadth to both text and painting, etc. However, why would we do that?
This kind of mathematical art can be seen as an attempt to eliminate indeterminacy in text, painting, music, etc. Thus, the fundamental simplicity of the statement-speech-exposure makes the creative act clearer.

Figure 13. Radoslav Rochallyi, 2022. -
Axiomatic Poetry: As the name suggests, Axiomatic Poetry deals with axioms, i.e., statements that serve as a starting point from which other statements logically follow. Truth or falsity does not weigh the creation of this poetry. The important thing is that the sentence follows the sentence. Unlike atomistic poetry, sentences or statements do not have to be clear and transparent. They can be like capturing feelings or consciousness, as it happens in the author of this poetry. We do not think it is necessary to follow the formal notation, although we find it interesting in this case so we will use it.

Figure 14. Radoslav Rochallyi, 2022. Set Poetry: Set Poetry uses sets as a collection of feelings, relationships, and statements. It is not essential to have semantic clarity, but it is important to be related. Of course, we are not talking about a real relationship, but the reader should understand why individual terms and expressions are together in a set.
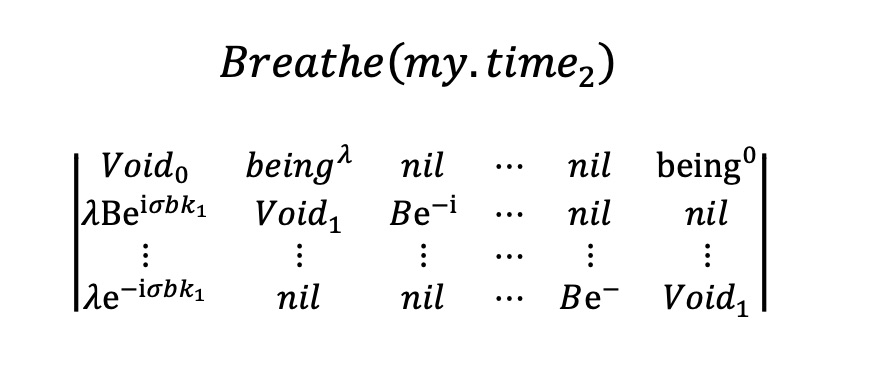
Figures 15 and 16. Radoslav Rochallyi, 2022. “My time.” # mathaeata, 2021, ISBN: 978-8097373719
Conclusion
All the above examples can also be applied to Equatorial poetry, although in the case of geometric poetry, topology, vectors, etc., visual use is more effective and not equational. We believe that the ambition of equational poetry should not necessarily be to preserve the meaning of the equation but to preserve the form, formula, and symmetry as precisely as possible. Preserving its whole meaning would define the content of the poetry and not just the form. In that case, we would not even be doing poetry because the resulting poem would be a cluster of precisely placed words without a general meaning. Moreover, we would not create anything mathematical, as we will surely recognize. However, at the same time, it must be said that there are many equations where we can place the text in such a way that it also has meaning and while the meaning of the equation as such is preserved (even if not in the complete mathematical sense).
We can say that we can apply poetry to all kinds of mathematics. Besides geometric poetry, which is at least 150 years old, we have many other possibilities.
We can use algebraic formulas and equations to create a unique form of poetic expression, including linear equations or quadratic equations in the presentation.
We can write trigonometric poetry and include sine, cosine, and other trigonometric equations in the author's expression.
We can even create the poetry of probability and statistics. Use probability and statistics and include the use of random variables and distributions. We can use topologies and fractal dimensions, and equations.
References
Quine, W. (1970). “Philosophy of Logic.” In Simon Blackburn & Keith Simmons (eds.), Truth. Oxford University Press.
Rochallyi, R. (2021). MAA Blog: Equation Poetry — MATH VALUES. mathvalues.org/masterblog/equation-poetry
Dobson, J.E., 2022. “Vector hermeneutics: On the interpretation of vector space models of text.” Digital Scholarship in the Humanities 37, 81–93. doi:10.1093/llc/fqab079.
Sondheim, Alan (2001). “Introduction: Codeworks.” American Book Review vol. 22, no.6.
Breeze, MEz. “Internal damage report.” Cauldron and Net. studiocleo.com/cauldron/volume2/features/mez/internal/idr1.htm